A Primer on Linear Regression and its Associated Misconceptions

Welcome to the new year and the first Prophage blog post for 2016! This is already looking like it will be a great year for science and blogging. But enough with the pleasantries, let's dive into some science.

I wanted to start the year off with post about math. I know, I know, math is an intimidating way to start the year, but don't run off yet! I swear that this will be painless and we will even learn something new! We are going to keep things simple and focus on an elegant paper that presents some misconceptions about a complicated topic. This topic is multiple linear regression. My goal is to introduce you to the topic of linear regression and prepare you to read this week's paper.

What is Linear Regression & When Should I Use It?

Before we talk about multiple linear regression, let's cover simple linear regression. In its most simplified form, linear regression is a method for modeling the interaction between an independent (i.e. explanatory) and dependent variable. This is often plotted as a scatter plot with the dependent variable on the y axis, the independent variable on the x axis, and the linear regression model drawn as a line (see figure below). 

We commonly use this approach when we want to predict a dependent value given an independent value. An example of this (in the plot below) is tree age vs diameter. We know that tree diameter depends on age, but what if we want to predict the diameter (dependent variable) of a tree at a given age (independent explanatory variable). We can perform a linear regression to create a simple predictive model (shown as the line) to tell us what the diameter is likely to be at a given age. In our example, at age 30 it looks like the tree diameter will be 5 inches. The slope of the line is a coefficient that represents the relationship between the explanatory (age) and dependent (diameter) variables.

What is Multiple Linear Regression & When Should I Use It?

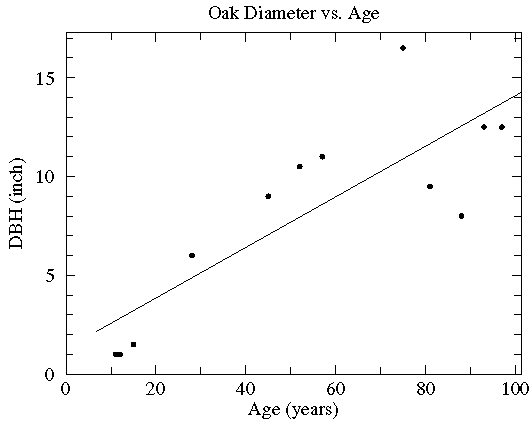A simple example of linear regression modeling.
Here we are modeling the relationship between
tree age and diameter. SOURCE

Now what if we want a better model that includes more than one explanatory variable. For instance, what if we want to predict tree diameter given it's age and the average summer temperature of the climate the tree lives in? We might expect a tree in a colder climate to have less of a diameter compared to a tree in a warm climate. Once we start considering more than one variable, we are doing a multiple linear regression. It's that simple. Much like in a simple linear regression, both explanatory variables (age and temperature) have a coefficient that represents the relationship between the explanatory and dependent variable. Think of this relationship coefficient as the slope for each explanatory variable.

What is the Misconception?

As Frasier TR expertly points out, there is a lot of confusion around interpreting these relationship coefficients. People often interpret these as being the independent relationships between the explanatory variables (age and temperature) and the dependent variable (diameter) given the full range of values of the explanatory variables. This is unfortunately not true. These coefficients only represent the relationship (i.e. slope) between their associated independent variable and dependent variable when the other independent variable is zero. So to use our example, the coefficient associated with age only represents the relationship (slope) between age and diameter when the temperature is zero. Frasier expertly outlines why this is actually a nontrivial point that has likely led to many erroneous scientific conclusions. Frasier's explanation is incredibly well done so I will direct you to followup with this post by reading the paper and seeing his examples for why this distinction is important.

Wrapping It Up

I know this was a math heavy post, but I hope you enjoyed it and even learned a little. After reading these brief paragraphs, you should have a general feel for what linear regression is and why it is useful. This will prepare you to dive into the Frasier paper that is absolutely with a read. And of course, I want to end by pointing out that this is a complicated topic that you can read entire books about. We did not even scratch the surface in this post, but at least we took the first step toward a better understanding of math and how it can be used for prediction.

Questions, comments, or concerns? Want to discuss any of these points? Add a comment below. I would love you hear what you think.

Works Cited

Frasier TR (2015). A note on the use of multiple linear regression in molecular ecology. Molecular ecology resources PMID: 26650184